مدلسازی چرخه سلولی | مکانیسم action potential

فهرست مطالب نمایش

چرا باید دینامیک چرخه سلولی را درک کنیم؟

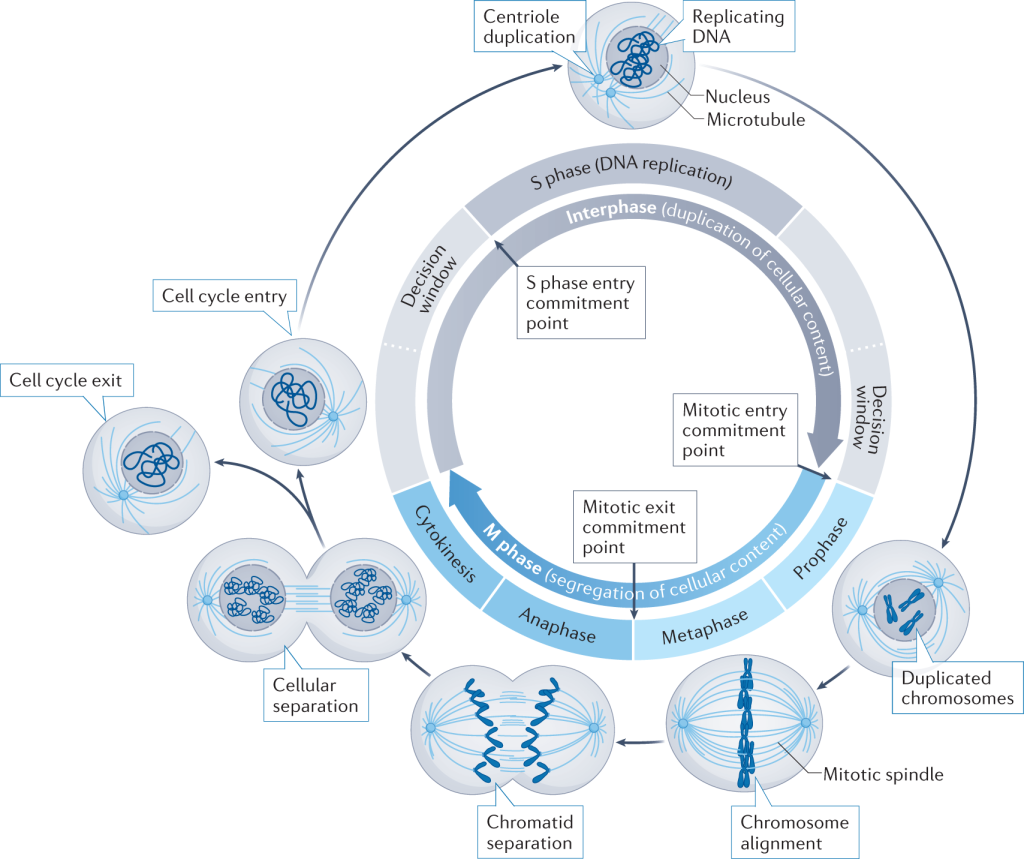
چرخه سلولی مکانیسمی است که مراحل سنتز DNA، میتوز و تقسیم سلولی را کنترل و یکپارچه می‌کند. این مکانیسم رشد سلول و همچنین تولیدمثل را به سلول دیکته می‌کند. بنابراین، به دست آوردن درک کامل از چرخه سلولی در سطح مولکولی برای درک نه تنها انسان، بلکه همه یوکاریوت‌ها حیاتی است. ایجاد دانش جامع از مدلسازی چرخه سلولی یکی از مهمترین اهداف حوزه زیست‌شناسی سلولی است.

همانطور که زیست‌شناسان بیشتر در مورد شبکه پیچیده کنترل چرخه سلولی صحبت می‌کنند، دانشمندان این حوزه نیز به دنبال بررسی تغییرات در این چرخه هستند. در حقیقت آن‌ها می‌خواهند بدانند که با تغییر در یک بخش این سیستم پیچیده، آیا می‌توانند رفتار چرخه را پیش‌بینی کنند یا آن را بهتر مطالعه کنند یا نه. با این حال، این پیش‌بینی‌ها برای به دست آوردن درک چگونگی انحراف از چرخه سلولی طبیعی منجر به بیماری ضروری هستند. این دانش می‌تواند در تعمیق دانش ما در مورد سرطان و همچنین توسعه راهبردهای درمانی و پیشگیری موثر جدید بسیار مهم باشد.

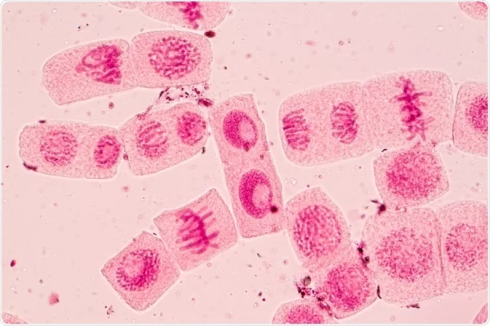
استفاده از مدل‌سازی ریاضی برای درک و مدلسازی چرخه سلولی

در حالی که مدل‌سازی ریاضی به عنوان یک روش تجربی سنتی در نظر گرفته نمی‌شود، اما ابزاری با پتانسیل برای کشف جزئیات ریزشبکه‌های پیام‌رسان سلولی پیچیده درگیر در مدیریت چرخه تقسیم سلولی یوکاریوتی هستند.

مدل‌های ریاضی قادر به سازماندهی مجموعه داده‌های بزرگ به دست آمده از مطالعات تجربی هستند. نشان داده شده است که آنها قادر به استفاده از این داده‌های تجربی برای توصیف اصول سیستم چرخه سلولی و همچنین پرکردن شکاف‌هایی هستند که داده‌ها در ارائه پاسخ ناکام مانده‌اند. مدل‌های ریاضی به‌طور باورنکردنی برای توسعه فرضیه‌ها مفید هستند و به راهنمایی دانشمندان برای کشف مسیرهایی که بیشترین پتانسیل را دارند کمک می‌کنند.

در حال حاضر، زمینه های علمی متمایز، مانند مهندسی شیمی و هواشناسی، مزایای استفاده از مدل‌سازی ریاضی برای کشف رفتارهای سیستم‌های پیچیده را نشان داده‌اند. با این حال، تا همین اواخر، مدل‌سازی ریاضی در زمینه زیست‌شناسی مولکولی کمتر مورد توجه قرار گرفته بود. خوشبختانه، سال‌های اخیر دانشمندانی حضور داشته‌اند که در این رشته از مدل‌سازی ریاضی کار می‌کنند تا بینش‌های کلیدی در مورد دینامیک و مدلسازی چرخه سلولی را آشکار کنند.

bistability یا دوپایداری یک مکانیسم رایج برای اطمینان از انتقال قوی و برگشت‌ناپذیر چرخه سلولی است. هر زمان که پارامترهای بیولوژیکی یا شرایط خارجی به گونه‌ای تغییر کند که از آستانه عبور کند، سیستم به طور ناگهانی بین حالت‌های مختلف چرخه سلولی جابجا می‌شود. مطالعات تجربی مکانیسم‌هایی را کشف کرده‌اند که می‌توانند شکل منحنی پاسخ دوپایا را به صورت پویا در زمان تغییر دهند. یک سوئیچ bistability می‌تواند کنترل بهتری روی زمان انتقال چرخه سلولی برای سلول فراهم کند.

بسیاری از سیستم‌ها در طبیعت دارای دوپایداری هستند، به این معنی که می‌توانند تحت شرایط یکسان به یکی از دو حالت پایدار پایدار تکامل یابند. اینکه آنها به کدام حالت تکامل می‌یابند بستگی به این دارد که سیستم از کجا آمده است. چنین دوپایداری bistability زیربنای رفتار سوئیچینگ است که برای پیشرفت سلول‌ها در چرخه تقسیم سلولی ضروری است. یک سوئیچ سریع زمانی اتفاق می‌افتد که سلول از یک حالت پایدار به حالت ثابت دیگر می‌پرد. مشخصه این رفتار سوئیچینگ، استحکام و برگشت ناپذیری آن است.

کشف الگوهای رشد نوسانی

تکثیر سلول‌ها برای اطمینان از فرآیندهای بیولوژیکی طبیعی حیاتی است، همچنین زمینه‌ساز فرآیندهای پاتولوژیک است. از زمانی که مدل‌های ریاضی برای اولین بار توسط زیست‌شناسی مولکولی مورد توجه قرار گرفت، مدل‌های متعددی از تکثیر سلولی ایجاد شده است. با این حال، این مدل‌ها اغلب فرض می‌کنند که تکثیر سلولی نمایی است و آن را در مدلسازی چرخه سلولی دخیل می‌کنند.

در مورد سلول‌های سنکرون، تقسیم در مراحل مجزا اتفاق می‌افتد و بنابراین نرخ رشد تولید شده سرانه متغیر است، نه نمایی. بنابراین، مدل‌هایی که قبلاً برای توصیف پویایی چرخه سلولی ایجاد شده‌اند، زیرجمعیت‌ها را در نظر نمی‌گیرند و رشد نمایی را پیش‌بینی می‌کنند که همیشه اینطور نیست.

سلول‌های سنکرون کشت میکروبیولوژیکی یا کشت سلولی است که حاوی سلول هایی است که همه در یک مرحله رشد هستند. از آنجایی که عوامل متعددی بر چرخه سلولی تأثیر می‌گذارند (بعضی از آنها تصادفی هستند)، کشت‌های طبیعی دارای سلول‌هایی در تمام مراحل چرخه سلولی هستند.

یک مطالعه در سال 2019 داده‌های تجربی جدیدی را ارائه کرد که از روش‌های تکثیر سلولی دو بعدی جمع‌آوری شده بود، جایی که رشد سلولی مشاهده‌شده به نظر نمایی بود. این تیم توانست ثابت کند که زیرجمعیت های نوسانی از چیزی که محققان به عنوان همگام‌سازی ذاتی (inherent synchronization) یاد می‌کنند به وجود آمده‌اند. این مطالعه از نشانگر چرخه سلولی مبتنی بر یوبی‌کوئیتیناسیون فلورسنت (FUCCI) برای شناسایی زیرجمعیت‌ها بر اساس فاز چرخه سلولی استفاده کرد و همگام‌سازی ذاتی را که معمولاً پنهان است، آشکار کرد.

این داده‌های کلیدی نشان می‌دهند که در حالیکه به نظر می‌رسد جمعیت‌های سلولی به‌طور تصاعدی رشد می‌کنند، ممکن است حاوی زیرجمعیت‌هایی باشند که به دلیل همگام‌سازی ذاتی، رشد نوسانی را نشان می‌دهند.

این تحقیق این واقعیت را برجسته می‌کند که مدل‌سازی ریاضی قبلی چرخه‌های سلولی کل را به تصویر نمی‌کشد، زیرا آنها زیرجمعیت‌هایی با رشد نوسانی را در نظر نمی‌گرفتند. مدل جدید ایجاد شده از طریق این تحقیق احتمالاً برای درک مکانیسم‌هایی که به چرخه سلولی وابسته هستند، مانند پاسخ به درمان‌ها، مفید خواهد بود. پس این رویکرد باید در مدلسازی چرخه سلولی وارد شود.

استفاده از مدل‌سازی ریاضی برای آشکار کردن پویایی چرخه سلولی تومورها

تحقیقات جدیدتر از مدل‌سازی ریاضی برای آشکار کردن ویژگی‌های کلیدی چرخه سلولی تومورها استفاده کرده است که ممکن است منجر به درمان‌های مؤثرتر سرطان شود.

در انکولوژی، اسفروئیدهای تومور (tumor spheroids) معمولاً به عنوان یک سنجش آزمایشگاهی برای بررسی چگونگی پاسخ رده‌های سلولی مختلف سرطانی به درمان‌ها استفاده می‌شوند. آنها بیشتر به دلیل نحوه رشد اسفروئیدها محبوب شده‌اند، با سلول‌های تومور که اکسیژن و مواد مغذی را در محیط کشت مصرف می‌کنند و باعث تکثیر سلولی موضعی در مرز spheroid می‌شوند.

سلول‌های مرکز spheroid با رشد spheroid هیپوکسیک می‌شوند و در نهایت می‌میرند و یک هسته نکروزه ایجاد می‌کنند. تکثیر موضعی سلول‌های تومور در سطح فشاری را ایجاد می‌کند که جریان سلولی سلول‌های تومور را ایجاد می‌کند که از لبه تومور منشا گرفته و به سمت هسته حرکت می‌کند. مطالعات نشان داده‌اند که این جریان به میکروسفرهای بی‌اثر اجازه می‌دهد تا وارد سطح شوند.

در یک مطالعه در سال 2020، دانشمندان این مدل را با استفاده از یک مدل مبتنی بر عامل ترکیبی خارج از شبکه مورد ارزیابی مجدد قرار دادند و تلاش کردند تا تعیین کنند که این میکروسفرها تا چه حد می‌توانند برای توصیف پارامترهای جنبشی مرتبط با spheroid مورد استفاده قرار گیرند.

محققان دریافتند که نرخ‌های متفاوت تکثیر سلول‌های تومور و حساسیت به هیپوکسی می‌تواند spheroidهایی ایجاد کند که دینامیک رشد توده‌ای مشابهی دارند اما ترکیبات داخلی بسیار متفاوتی دارند. این تیم از شواهد خود برای تولید مدلی استفاده کرد که می تواند برای استنباط ترکیب spheroid و پارامترهای مربوط به رده‌های سلولی تومور مورد استفاده قرار گیرد و ناکارآمدی مدل‌های قبلی را که بر محاسبات دیگر تکیه داشتند، برجسته کند. این نتایچ با مدلسازی چرخه سلولی به دست آمده است.