دستهبندی نشده
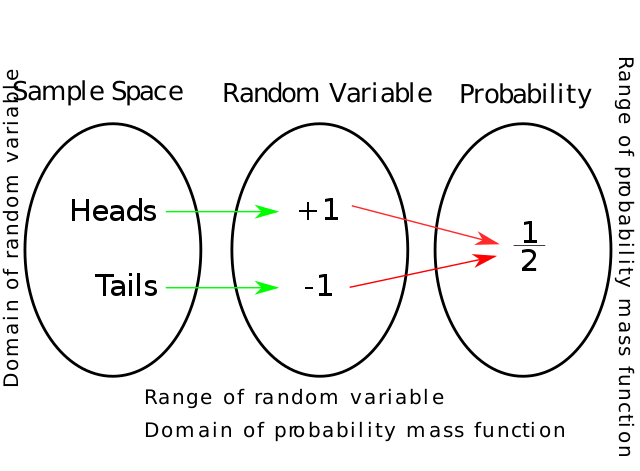
متغیر تصادفی
مقدمهای بر متغیر تصادفی
متغیر تصادفی یک توصیف عددی از نتیجه یک آزمایش آماری است. به متغیر تصادفی که ممکن است فقط یک عدد محدود یا یک دنباله نامتناهی از مقادیر را فرض کند گسسته گفته می شود. به متغیر تصادفی که ممکن است هر مقداری را در یک بازه در خط اعداد واقعی فرض کند، پیوسته گفته می شود. به عنوان مثال، یک متغیر تصادفی که تعداد خودروهای فروخته شده در یک نمایندگی خاص در یک روز را نشان می دهد، گسسته خواهد بود، در حالی که یک متغیر تصادفی که وزن یک فرد را بر حسب کیلوگرم (یا پوند) نشان می دهد، پیوسته خواهد بود.
امید ریاضی
امید ریاضی دقیقاً همان چیزی است که ممکن است به طور شهودی فکر کنید: بازدهی که می توانید برای نوعی عمل انتظار داشته باشید، مانند تعداد سؤالاتی که ممکن است در صورت حدس زدن در یک آزمون چند گزینه ای درست به دست آورید. در آمار و تحلیل احتمال، امید ریاضی با ضرب هر یک از نتایج ممکن در احتمال وقوع هر نتیجه و سپس جمع کردن همه آن مقادیر محاسبه می شود. با محاسبه مقادیر مورد انتظار، سرمایه گذاران می توانند سناریویی را انتخاب کنند که به احتمال زیاد نتیجه مطلوب را به همراه دارد.
واریانس
اصطلاح واریانس به اندازهگیری آماری پراکندگی بین اعداد در یک مجموعه داده اشاره دارد. به طور خاص، واریانس اندازهگیری میکند که هر عدد در مجموعه چقدر از میانگین و بنابراین از هر عدد دیگری در مجموعه فاصله دارد. واریانس اغلب با این نماد نشان داده می شود: σ2. جذر واریانس نیز انحراف معیار (σ) است.
CDF, PDF, PMF
توزیع احتمال برای یک متغیر تصادفی نحوه توزیع احتمالات بر روی مقادیر متغیر تصادفی را توصیف می کند. برای یک متغیر تصادفی گسسته، x، توزیع احتمال با یک تابع جرم احتمال یا PMF تعریف میشود. این تابع احتمال هر مقدار از متغیر تصادفی را فراهم می کند. در توسعه تابع احتمال برای یک متغیر تصادفی گسسته، دو شرط باید برآورده شود: (1) تابع باید برای هر مقدار متغیر تصادفی غیرمنفی باشد و (2) مجموع احتمالات برای هر مقدار متغیر تصادفی باید برابر با یک باشد.
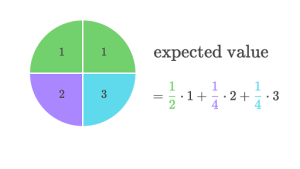
یک متغیر تصادفی پیوسته ممکن است هر مقدار را در بازهای روی خط اعداد واقعی یا مجموعهای از بازهها در نظر بگیرد. از آنجایی که تعداد نامتناهی مقادیر در هر بازه ای وجود دارد، صحبت در مورد احتمال اینکه متغیر تصادفی مقدار خاصی به خود بگیرد، معنی ندارد. در عوض، احتمال اینکه یک متغیر تصادفی پیوسته در یک بازه معین قرار گیرد در نظر گرفته می شود.
در حالت پیوسته، همتای تابع جرم احتمال، تابع چگالی احتمال یا PDF است که با f(x) نیز نشان داده می شود. برای یک متغیر تصادفی پیوسته، تابع چگالی احتمال ارتفاع یا مقدار تابع را در هر مقدار خاص x ارائه میکند. این تابع به طور مستقیم احتمال اینکه متغیر تصادفی مقدار خاصی را دریافت کند را نمی دهد.
با این حال، مساحت زیر نمودار f(x) مربوط به یک بازه، که با محاسبه انتگرال f(x) در آن بازه به دست میآید، این احتمال را فراهم میکند که متغیر در آن بازه مقداری به خود بگیرد. یک تابع چگالی احتمال باید دو شرط را برآورده کند: (1) f(x) باید برای هر مقدار متغیر تصادفی غیرمنفی باشد و (2) انتگرال روی همه مقادیر متغیر تصادفی باید برابر با یک باشد.
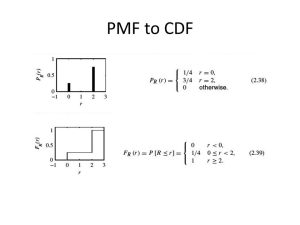
تابع توزیع تجمعی (CDF) یک متغیر تصادفی روش دیگری برای توصیف توزیع متغیرهای تصادفی است. تابع توزیع تجمعی این احتمال را توصیف می کند که یک متغیر تصادفی X با توزیع احتمال معین در مقداری کمتر یا مساوی x پیدا شود. مزیت CDF این است که می توان آن را برای هر نوع متغیر تصادفی (گسسته، پیوسته) تعریف کرد.
توزیع ها
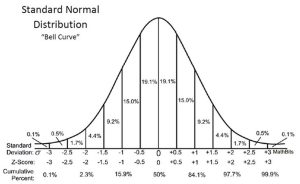
نمونه ای از داده ها یک توزیع را تشکیل می دهد و تا حد زیادی شناخته شده ترین توزیع، توزیع گاوسی است که اغلب توزیع نرمال نامیده می شود. توزیع یک تابع ریاضی پارامتری را ارائه می دهد که می تواند برای محاسبه احتمال هر مشاهده فردی از فضای نمونه استفاده شود. این توزیع، گروه بندی یا چگالی مشاهدات را که تابع چگالی احتمال نامیده می شود، توصیف می کند. همچنین میتوانیم احتمال اینکه یک مشاهده دارای مقداری مساوی یا کمتر از مقدار معین باشد را محاسبه کنیم.
یکی از توزیع های معروف توزیع نرمال است. توزیع نرمال که با نام توزیع گاوسی نیز شناخته می شود، یک توزیع احتمال متقارن نسبت به میانگین است، که نشان می دهد احتمال وقوع داده های نزدیک به میانگین بیشتر از داده های دور از میانگین هستند. در شکل نمودار، توزیع نرمال به صورت منحنی زنگوله ای ظاهر می شود.
مطالعات بیشتر در بخش راهنمای علمی سایت
کاراموزی های بیشتر در بخش کاراموزی های سایت